This is a very concise introduction to some of the concepts involved in subpavings using descriptions given in the introductory text book "Applied Interval Analysis", by Jaulin, Kieffer, Didrit and Walter; Springer, 2001. This book is abbreviated by AIA2001.
For a full description of subpavings see AIA2001 http://www.lss.supelec.fr/books/intervals/
An interval real [x] (usually referred to simply as an interval [x]) is a connected subset of the reals R. An interval has an upper bound and a lower bound. [AIA2001, pp. 18-20]
An interval vector [x] is a subset of Rn (n-dimensional space) that can be defined as the cartesian product of n closed intervals. [x] is usually referred to as an interval vector or box. IRn is the set of all closed intervals of Rn. [AIA2001, p. 23]
Given a function x from Rn to Rm, the interval function [f] is an inclusion function for f if, for all [x] in IRn, f([x]) is a subset of [f]([x]). The inclusion function f makes it possible to compute a box [f]([x]) guaranteed to contain f([x]). [AIA2001, p. 27]
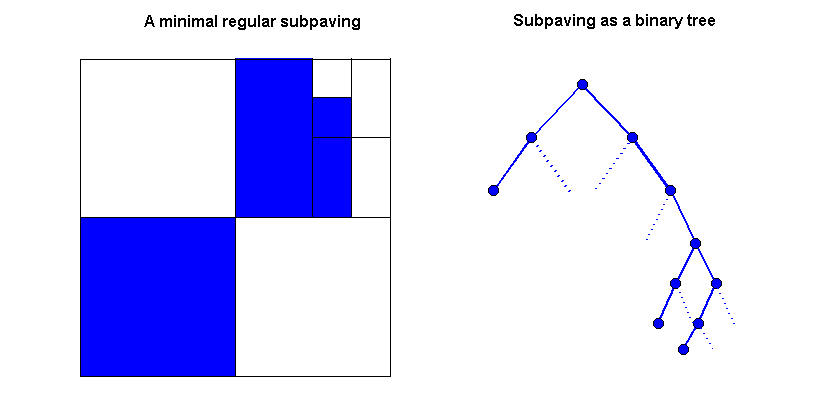
A subpaving of a box [x] is a union of non-overlapping subboxes of [x]. [AIA2001, p. 48]. To form this subpaving we subdivide [x] and then subdivide the subboxes, and then subdivide those subboxes . . . The definition of a subpaving also allows us to not select some subbox resulting from any subdivision in the subpaving (only the subboxes we keep can be further subdivided, of course).
Bisection of a box is subdivision of the box in half along its longest dimension (or the first longest dimension if it has the same longest length in more than one dimension). In one dimension, bisection is dividing an interval in half. In two dimensions, bisection is drawing a line through the middle of a rectangle, normal to its longest dimension. In three dimensions bisection is slicing a plane through a box, again normal to its longest dimension and again in order to divide the box in half. In general, in n dimensions, bisection is by an (n-1)-dimensional hyperplane normal to the longest dimension of the box at the midpoint of the box on that longest dimension.
A regular subpaving is obtained from a finite succession of bisections and selections. It is computationally simpler to perform operations, such as intersection, on regular subpavings than on non-regular subpavings and so they are more easily manipulated in computer applications [AIA2001, pp. 49-50].
A regular subpaving can be represented as a binary tree. Bisection of a box into two subboxes corresponds to the node representing that box branching to two child nodes. A decision not to include a subbox in the subpaving means that that branch is pruned off the tree. Thus the growth of the branches is defined by how the initial box, which corresponds to the root of the tree, is bisected and which boxes are selected. A node with no children is a degenerate node or leaf, and represents a box that is not subdivided. In the tree representation of the subpaving, a leaf indicates that the box it represents belongs to the subpaving. A tree (or the subpaving it represents) is minimal if it has no sibling leaves; that is, no node has more than one leaf-child. [AIA2001, p. 52]. The presence to two sibling leaves (which means that the subpaving is non-minimal) indicates that a box is subdivided and both subboxes (child nodes) retained.
Jaulin, Kieffer, Didrit and Walter use regular subpavings for set computation. In particular, the computation of a reciprocal image X = f-1(Y) where Y is regular subpaving of Rm (set inversion), and computation of the direct image of a subpaving Y = f(X) where X is a regular subpaving of Rn (image evaluation). [AIA2001] outlines the creation of a SUBPAVINGS class and the implementation their algorithms using this class for set inversion and image evaluation in C++ given some library for interval analysis: the basic requirements of such an interval analysis library are given and their own implementation uses the PROFIL/BIAS library. We have implemented the algorithms for set inversion and image evaluation using the C-XSC interval library with as little change to the structure and code used in [AIA2001] as possible, other than that necessitated by the use of C-XSC.
See:
Our interest in subpavings is more general than set computation in the sense of Regular subpavings and set computation. Regular subpavings represent a special case of the general kd tree structure: a space partitioning data structure for organising points in k-dimensional space. We aim to combine interval analysis and inclusion functions with kd trees and manipulation of tree structures. In particular, we are interested in the use of subpavings for statistical set processing.
We start with a re-implemention in C++ of the subpaving-as-a-binary-tree class based on [AIA2001]. Again, we use C-XSC as the interval analysis library. We alter the structure of the class and functions to give us a better basis for using the class as a base class for derived classes specifically for statistical set processing. See Subpavings as a basis for statistical set processing.
We extend this base class to a class specifically designed for processing statistical sample data. The subpaving becomes a way to organise and summarise the sample data. The boxes of the subpaving can be thought of a 'buckets' for the data points contained in its interval vector box. The binary tree representation of the subpaving shows how the subpaving has been formed. Each node in the tree can maintain summaries (such as count, and sum) of the data it represents. See Subpavings for processing statistical sample data. The statistical subpaving class is used in our work on Adaptive histograms by extending the algoritthms and data structures in Regular subpavings and set computation .
See: